L2

from [1] CHAPTER 7. REGULARIZATION FOR DEEP LEARNING

在二次方程中，

\[\begin{align} \tilde{\boldsymbol{w}} &=\left(\boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top}+\alpha \boldsymbol{I}\right)^{-1} \boldsymbol{Q} \mathbf{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \\ &=\left[\boldsymbol{Q}(\boldsymbol{\Lambda}+\alpha \boldsymbol{I}) \boldsymbol{Q}^{\top}\right]^{-1} \boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \\ &=\boldsymbol{Q}(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \end{align}\]

$\alpha$ 是正则化系数，系数对$\Lambda$中系数越大的效果越小，可以看到，随着$\alpha$的增大，首先抹去的是小的系数。$\frac{\lambda _i}{\lambda_i + \alpha}$

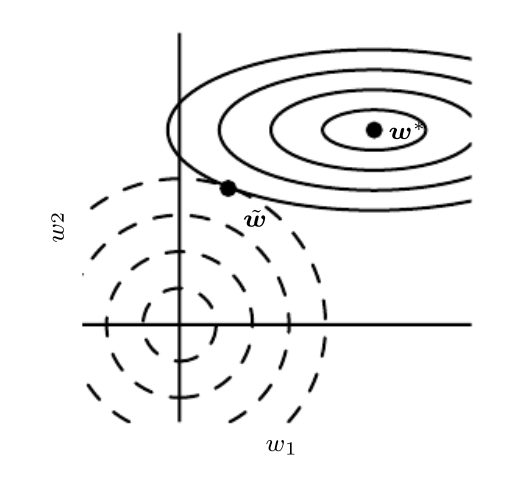
图里可以看到，正则化梯度等高线以零为原点，$w$则以$w^{*}$为原点。两者相切时候，hessian矩阵越大的，保留的$w$越大。不过也相当于有一点点用，一般就不会衰减到零

L1

\[\hat{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})=J\left(\boldsymbol{w}^{*} ; \boldsymbol{X}, \boldsymbol{y}\right)+\sum_{i}\left[\frac{1}{2} H_{i, i}\left(\boldsymbol{w}_{i}-\boldsymbol{w}_{i}^{*}\right)^{2}+\alpha\left|w_{i}\right|\right]\] \[\begin{align} \frac{d \hat{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})}{dw_i}&= H_{i, i}\left(\boldsymbol{w}_{i}-\boldsymbol{w}_{i}^{*}\right)+\alpha\operatorname{sign}\left(w_{i}\right)\\ \end{align}\]

let $\frac{d \hat{J}(\boldsymbol{w} ; \boldsymbol{X}, \boldsymbol{y})}{dw_i} = 0$

then

\(\begin{align} 0 &= H_{i, i}\left(\boldsymbol{w}_{i}-\boldsymbol{w}_{i}^{*}\right)+\alpha\operatorname{sign}\left(w_{i}\right)\\ H_{i, i}w_i &= H_{i, i}w_{i}^{*}-\alpha\operatorname{sign}\left(w_i\right)\\ w_i &= w_{i}^{*}-\frac{\alpha\operatorname{sign}\left(w_i\right)}{H_{i, i}} \label{a} \end{align}\) ​

公式$\ref{a}$ 推到公式$\ref{b}$就是分析了，$w_i > 0$时如何如何，$w_i^*<0$时如何如何。

\[\begin{equation} w_{i}=\operatorname{sign}\left(w_{i}^{*}\right) \max \left\{\left|w_{i}^{*}\right|-\frac{\alpha}{H_{i, i}}, 0\right\} \label{b} \end{equation}\]

$H_{i,i}$小的时候，会直接忽略$w_i$直接把他往零推。

injection noise at the hidden layer input(output) or the weights

\[\begin{equation} \epsilon_{\boldsymbol{W}} \sim \mathcal{N}(\boldsymbol{\epsilon} ; \mathbf{0}, \eta \boldsymbol{I}) \end{equation}\]

这个如何等价于加上正则化项 \(\eta \mathbb{E}_{p(\boldsymbol{x}, y)}\left[\left\|\nabla_{\boldsymbol{W}} \hat{y}(\boldsymbol{x})\right\|^{2}\right]\) ???

Injection noise at the output targets

​ 这个就是label smoothing。

Early stop

​ 挺好玩的是early stop 用二阶展开推导结果和l2正则化的二阶展开的推导形式是一致的。甚至参数都可以大致换算。

书上p248 推导

\[\begin{align} \boldsymbol{w}^{(\tau)}-\boldsymbol{w}^{*} &=\left(\boldsymbol{I}-\epsilon \boldsymbol{Q} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top}\right)\left(\boldsymbol{w}^{(\tau-1)}-\boldsymbol{w}^{*}\right) \label{11}\\ \boldsymbol{Q}^{\top}\left(\boldsymbol{w}^{(\tau)}-\boldsymbol{w}^{*}\right) &=(\boldsymbol{I}-\epsilon \boldsymbol{\Lambda}) \boldsymbol{Q}^{\top}\left(\boldsymbol{w}^{(\tau-1)}-\boldsymbol{w}^{*}\right) \label{12} \end{align}\]

中间推导过程

其实就是公式$\ref{11}$带入到公式$\ref{12}$里面去，并且$w^{\left(0\right)}=0$。小技巧是$1+\tau -1 = \tau$所以最后推到$w$右上角系数为0时，昨天乘号系数就知道了。

\[\begin{align} \boldsymbol{w}^{(\tau)}-\boldsymbol{w}^{*} &=\boldsymbol{Q}\left(\boldsymbol{I}-\epsilon \boldsymbol{\Lambda} \right)\boldsymbol{Q}^{\top}\left(\boldsymbol{w}^{(\tau-1)}-\boldsymbol{w}^{*}\right) \\ &=\boldsymbol{Q}\left(\boldsymbol{I}-\epsilon \boldsymbol{\Lambda} \right)^{\tau}\boldsymbol{Q}^{\top}\left(\boldsymbol{w}^{(0)}-\boldsymbol{w}^{*}\right) \end{align}\]

$w^{(\tau -1)}$代入到公式$\ref{12}$里面，即得下面的结果。

中间推导过程

\[\begin{equation} \boldsymbol{Q}^{\top} \boldsymbol{w}^{(\tau)}=\left[\boldsymbol{I}-(\boldsymbol{I}-\epsilon \boldsymbol{\Lambda})^{\tau}\right] \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \end{equation}\]

下面两个公式$\ref{equ:ori}$和$\ref{equ:after}$的推导其实就是用公式$\ref{equ:exten}$乘法展开

\[\begin{align} (\boldsymbol{\Lambda}+\alpha \boldsymbol{I})(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} = \boldsymbol{I} \label{equ:exten} \end{align}\] \[\begin{align} \boldsymbol{Q}^{\top} \tilde{\boldsymbol{w}} &=(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} \boldsymbol{\Lambda} \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \label{equ:ori}\\ \boldsymbol{Q}^{\top} \tilde{\boldsymbol{w}} &=\left[\boldsymbol{I}-(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} \alpha\right] \boldsymbol{Q}^{\top} \boldsymbol{w}^{*} \label{equ:after} \end{align}\]

最终学习率$\tau$，更新次数$\epsilon$，正则化参数$\alpha$可以用下面的公式推

\[\begin{align} &\tau \approx \frac{1}{\epsilon \alpha} \label{19}\\ &\alpha \approx \frac{1}{\tau \epsilon} \label{20} \end{align}\]

公式$\ref{20}$和$\ref{19}$通过公式$\ref{ori}$推导，通过$\log(1+x)$的泰勒公式序列展开就行，展开一项就能得到下面的结果，当然得附带一些远小于1的条件。很容易，这里就不写了。

\[\begin{equation} (\boldsymbol{I}-\epsilon \boldsymbol{\Lambda})^{\tau}=(\boldsymbol{\Lambda}+\alpha \boldsymbol{I})^{-1} \alpha \label{ori} \end{equation}\]

Sparse Representation

不仅是weight可以稀疏表示（l1正则），输出的representation也可以变稀疏。

Bagging and Other Ensemble Methods

​ 模型相关性得低，这才是关键。结果能推出来，误差与数量成反比。p253

Dropout

dropout 实现里好像是直接关闭dropout就能享用平均模型的效果了。但是根据这里的理解以及书上，应该dropout不能关，应该是多次预测取平均才行（即进行采样，求期望值）甚至要做成概率形式。如果直接关掉dropout，那么weight得乘以dropout的保留概率，使其数值大小大概一致。如果得关闭dropout得使dropout的输出保持一致。书上p261引用的论文，参数scaling甚至比上千个子网络采样平均还有用。

[1]

“https://www.deeplearningbook.org/contents/ml.html.” https://www.deeplearningbook.org/contents/ml.html (accessed Oct. 11, 2021).