算法面经整理
推荐系统
-
-
LFM MF SVD SVD++ FM difference
-
EVD: 特征值分解, $A=Q\Sigma Q^{-1}$, 在线性子空间,各个分量的大小。[1]
- SVD:适用于非方阵 [1]
- 一般来说SVD里的 \(M=U*\Sigma*V\), \(U \in R^{m*m}\), \(\Sigma \in R^{m*n}\), \(V \in R^{n*n}\) [2]
- 但是推荐系统里一般指compact SVD, \(U \in R^{m*k}\), \(\Sigma \in R^{k*k}\), \(V \in R^{k*n}\) [2, 3]
- 求解:通过求\(MM^T\) 和 \(M^TM\)的特征值,分别得到\(U\)和$V$。然后$\Sigma$由下式得到:$A=U \Sigma V^{T} \Rightarrow A V=U \Sigma V^{T} V \Rightarrow A V=U \Sigma \Rightarrow A v_{i}=\sigma_{i} u_{i} \Rightarrow \sigma_{i}=\frac{A v_{i}}{u_{i}}$
- 由于求解太复杂,所以有了compact SVD, 只保留前几个奇异值,同时效果还可以。
- 同时原始的SVD必须是要稠密矩阵,应用中实际上大量是空的,所以一般要均值填充或其他方法如下面的FunkSVD。
-
FunkSVD: 分解为两个矩阵,且只关心非空元素,同时有l2正则。[4]
\[\begin{equation} \min _{q^{*}, p^{*}} \sum_{(u, i) \in \mathcal{K}}\left(r_{u i}-q_{i}^{T} p_{u}\right)^{2} \end{equation}\] -
PMF:概率形式的FunkSVD, 参数符合正态分布。[4]
-
BiasSVD: 加入了用户和item的偏置,减少参数学习的难度。[4]
\[\begin{equation} \hat{r}_{i j}=\mu+b_{u}+b_{i}+q_{i}^{T} p_{u} \end{equation}\] -
SVD++: 加入了其他隐式反馈信息。其中$I_u$是隐式反馈行为的列表。并加入了隐式反馈行为对用户的偏好的影响$y_j$[4]
\[\begin{equation} \hat{r}_{u i}=\mu+b_{i}+b_{u}+q_{i}^{\top}\left(p_{u}+\left|I_{u}\right|_{j m}^{-\frac{1}{2}} \sum_{j \in I_{u}} y_{j}\right) \end{equation}\] -
timeSVD:用户的偏好等会随时间变化。$t$表示的时间相关参数。
\[\begin{equation} \hat{r}_{u i}=\mu+b_{i}\left(t_{u i}\right)+b_{u}\left(t_{u i}\right)+q_{i}^{T} p_{u}\left(t_{u i}\right) \end{equation}\] -
NMF:非负矩阵分解,做这个主要是由于分解出来的矩阵有负值的话,现实应用中很难解释推荐,如果都是正值就能较好解释了。
-
WMF:(只有正样本的分类问题叫One-class问题,论文:One-class collaborative filtering)加权的矩阵分解,以及负采样。
\[\begin{equation} \mathcal{L}(\boldsymbol{X})=\sum_{i j} W_{i j}\left(R_{i j}-X_{i j}\right)^{2} \end{equation}\] - LLORMA: 局部低秩,而不是全局低秩。???(Lee et al. Local low-rank matrix approximation.ICML. 2013.)
- adboost原理
-
focal loss:
\[\begin{equation} \operatorname{FL}\left(p_{\mathrm{t}}\right)=-\alpha_{\mathrm{t}}\left(1-p_{\mathrm{t}}\right)^{\gamma} \log \left(p_{\mathrm{t}}\right) \end{equation}\]
-
- 详细面经
- catboost
- [ ]
- 携程暑期实习 搜索推荐算法岗[5]
- 推荐系统流程
- 推荐系统各个阶段所用的模型:
- 召回 [6]
- 规则召回(兴趣标签top,热门top,新品top等)
- 协同召回
- 基于用户的协同过滤:喜欢相似物品的用户之间,存在着相似的兴趣偏好
- 应用场景与优缺点:
- 因为UserCF是基于用户相似度的推荐,所以它具备了非常强的社交属性,容易通过社交关系来传播符合用户口味的东西,因此它更适用于新闻推荐这样的场景,一方面新闻内容具有实时性、热点性,而UserCF更擅长于捕捉这一类的内容。另一方面,新闻内容的数量要远远多余用户数量,因此计算向量相似度时,要比ItemCF的时间复杂度更低。
- 新用户往往历史行为数据非常稀疏,可能会得到【0,0,0,0,0,…..,1】这样的向量,导致根据用户相似度推荐的物品准确度和置信度会非常低。也就是说如果遇到低频应用以及用户冷启动会比较麻烦,不太适用。
- 还有一种情况是,用户数远远多于商品数,用户数的不断增长会导致用户相似度矩阵难以维护,它用到的存储空间的增长速度是呈指数级的。
- 应用场景与优缺点:
- 基于商品的协同过滤: 用户偏好一类物品,喜欢物品的用户群相似的话,物品也会是相似的。
- 应用场景与优缺点:
- 因为UserCF有一些明显的缺点,所以Amazon和Netflix最早应用的都是ItemCF,它相比用户向量,物品的向量变化要更为稳定,因此广泛用于电商和视频推荐的领域,当用户对某一类商品或某一类电影产生兴趣时,此时给Ta推荐同类型的商品或电影是一个可靠的选择。
- ItemCF不具备很强的泛化能力。当一个热门商品出现后,它容易和大量的商品都具有相似性,导致推荐商品时,热门商品的出现概率会非常高,形成了“头部效应”,同样也致使处于长尾的商品较难被挖掘,因为长尾商品的特征向量会非常稀疏。所以要想解决这个问题,需要后期添加一些干预策略在里面。
- 应用场景与优缺点:
- 基于用户的协同过滤:喜欢相似物品的用户之间,存在着相似的兴趣偏好
- 向量召回
- FM召回
- Item2vec
- Youtube DNN向量召回,
- Graph Embedding召回,
- DSSM双塔召回: n-gram 分词后,使用Word hashing进行处理。反正就是两个分开的网络呗
- 粗排
- 精排
- 排序模型:
- GBDT + LR、
- Xgboost
- FM/FFM:后面那个就是加了个field,多个embedding
- Wide&Deep:
- DeepFM:就是将wide部分换成了fm模型,不用手工做特征了。
- Deep & Cross:cross层可以等价于FM模型,但是特征交叉的纬度更高。相当于n次多元方程,n小于等于cross的层数。
- DIN:聚合用户过往行为向量到的时候引入attention机制。其中attention根据过往行为向量与当前需要推荐的广告向量一起计算(两个向量相减的绝对值与两个向量的原始值进行拼接)。
- BST:用户行为序列+Transformer
- position embedding:直接使用原始的embedding效果不是很好。用了事件的时间戳作为embedding(但是我觉得还是得处理过,不能直接用的。) \(\begin{equation} \operatorname{pos}(v i)=\operatorname{timestamp}\left(v_{t}\right)-\operatorname{timestamp}\left(v_{i}\right) \end{equation}\)
- 作者还另外设计了交叉特征作为输入。
- 仅仅stack了一层,stack多层的效果并没有很好,反而下降了
- sequence长度仅仅20
- embedding size:4-64
- 召回 [6]
- 各阶段的目的:
- 召回:召回层的特点是:数据量大、速度响应快、模型简单、特征较少。因此召回层的意义在于缩小对商品的计算范围,将用户感兴趣的商品从百万量级的商品中进行粗选,通过简单的模型和算法将百万量级缩小至几百甚至几十量级。这样用户才能有机会在毫秒的延迟下,得到迅速的商品反馈。
- 粗排:得到精确的排序结果,也是推荐系统产生效果的重点,更是深度学习等应用的核心。从召回层召回的几百个物品,进行精准排序,根据规则对每个商品赋予不同的得分,由高至低来排序。由于精确度的要求,排序层的模型一般比较复杂,所需要的特征会更多。排序层的特点是:数据量少、排序精准、模型复杂、特征较多。
- 精排:业务排序层,这一环连接着排序层和即将给用户展示的推荐列表。物品在排序层排好序之后,不一定完全符合业务要求和用户体验,有时我们还需要兼顾结果的多样性、流行度、新鲜度等指标,以及结果是否符合当前产品发展阶段某些流量的倾斜策略等,实施特定的业务策略,来对当前已经排好序的物品进行再次排序。比如物品的提权、打散、隔离、强插等。举个实际的例子,一个内容平台,假设有A、B、C三类内容,我们不想让A类型的内容连续出现3次以上,就需要加一些干扰规则,将A类内容进行打散处理,使得用户最终看到的推荐列表是符合业务上的预期的。重排序的特点是:重业务需求、重用户体验。
- 指标[7]:
- NDCG:归一化折损增益,
- MRR:(Mean Reciprocal Rank) $k_u$ 是第一个相关item的位置: \(\operatorname{MRR}(O, U)=\frac{1}{|U|} \sum_{u \in U} \frac{1}{k_{u}}\)
- MAP: (Mean Average Precision)This is primarily an approximation of the original goal of the AP metric.
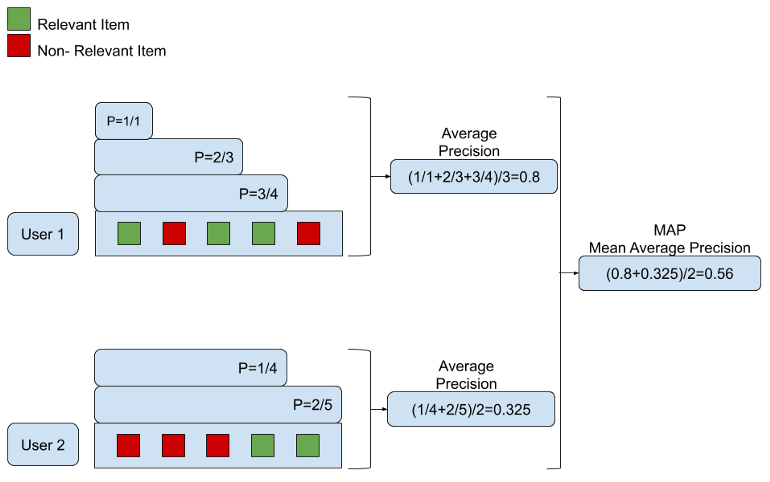
- NDCG: 可以使用标签里的相关性程度,而其他只能有相关和不相关。
- cons: 反馈不完整;IDCG等于零时处理;@k处理
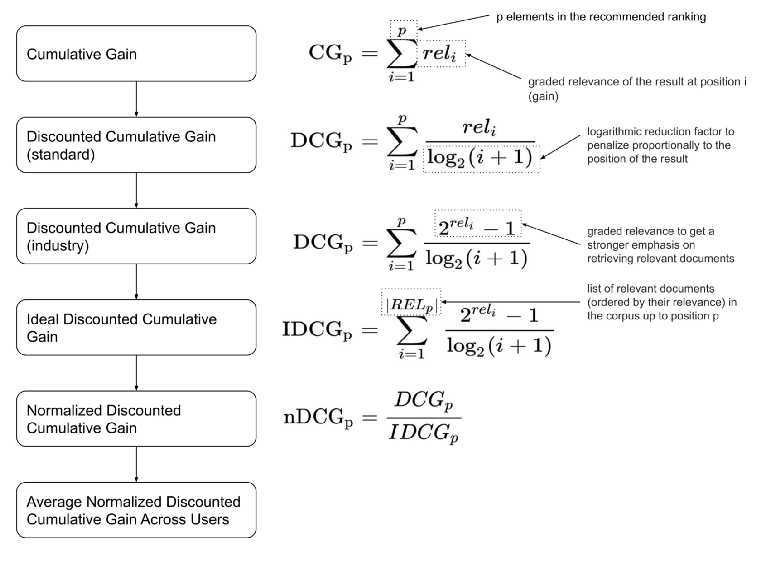
- cons: 反馈不完整;IDCG等于零时处理;@k处理
- The AP metric represents the area under the precision-recall curve.
- ROC曲线含义,坐标轴:对正负样本类别数量比例具有鲁棒性 [8]
- 坐标轴:Y:recall(真阳率),X: 假阳率 $\frac{\lvert Prediction - Positive \rvert}{\lvert negative \rvert}$
- PR曲线含义,坐标轴: 主要关心正例[8]
- 坐标轴:Precision - Recall
- 使用场景:[8]
- ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。
- 如果有多份数据且存在不同的类别分布,比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同,这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响,则ROC曲线比较适合,因为类别分布改变可能使得PR曲线发生变化时好时坏,这种时候难以进行模型比较;反之,如果想测试不同类别分布下对分类器的性能的影响,则PR曲线比较适合。
- 如果想要评估在相同的类别分布下正例的预测情况,则宜选PR曲线。
- 类别不平衡问题中,ROC曲线通常会给出一个乐观的效果估计,所以大部分时候还是PR曲线更好。
- 最后可以根据具体的应用,在曲线上找到最优的点,得到相对应的precision,recall,f1 score等指标,去调整模型的阈值,从而得到一个符合具体应用的模型。
- AUC:
- 召回怎么做
- 双塔模型优势,缺点,如何改进:
- 优点:速度快
- 缺点:精度低
- 改进: (1)减少特征信息损失:不再完全依赖DNN拟合能力,筛选重要特征参与交叉,减少无关特征干扰,或引入多种交叉网络(FM、DCN等),多种交叉方式取长补短,减少特征损失,如SENet双塔模型、并联双塔模型(2)蒸馏学习:以精排模型为teacher,指导双塔模型学习,通过蒸馏学习的方式,弥补双塔模型特征和结构上的不足(3)引入交叉信息或特征:
- 如何实现快速召回
- 粗排的目的是什么:
- wide&deep模型 为什么要有wide层结构,优缺点,如何改进?
- 缺点就是还是得手动特征工程。
- deepfm中的fm怎么做的
- 1 线下提升线上效果不好: 数据分布不同,有标签泄露啊,线上线下特征不一致啊
- 10 多路召回的作用:使用不同的召回策略,保证召回率的同时提升速度(可以并行召回)
- 21 推荐系统的特征工程有哪些?怎么做?
- 33 如何解决推荐系统重复推荐用户已经处理过的item的问题?推荐过的物品得记录下来,然后筛掉,可以用布隆过滤器。
- 34 推荐系统召回阶段如何实现热门item的打压?(推荐中的“哈利波特”效应):负采样
- 36 user/item冷启动怎么解决?:收集更多信息?
- 41 协同过滤,优缺点。
- 无需上下文,
- 无法添加其他特征,冷启动问题,
- 48 LR中连续特征为什么要做离散化?:非线性,便于特征交叉,模型鲁棒(防止特征过大),
搜索
NLP
机器学习
- 手推bp公式
- SVM(原理)[9]
- LR(为啥用sigmoid函数,交叉熵推导,MAE和MLP,反向传播,归一化,正则化)
- 降维算法(SVD和PCA)
- K-Means(手撕代码实现)
- 决策树(各种生成和剪枝方法):https://blog.csdn.net/pxhdky/article/details/84102660
- 集成学习(随机森林、XGBoost、AdaBoost、GBDT)
- EM算法(原理):https://zhuanlan.zhihu.com/p/40991784
- 过拟合(正则化、增加训练数据、数据增强、标签平滑、BatchNorm、Early-Stop、交叉验证、Dropout、Pre-trained、引入先验知识(贝叶斯,先验分布))
- 方差偏差分解(解释什么是方差什么是偏差,公式推导):https://zhuanlan.zhihu.com/p/38853908
- 正则化(L1和L2的会有啥现象、解释原因、分别代表什么先验:https://www.zhihu.com/question/23536142 , bias要不要正则:https://www.zhihu.com/question/66894061 )
- 初始化(不同网络初始化有啥区别:https://zhuanlan.zhihu.com/p/62850258 ,神经网络隐层可以全部初始化为0吗)
- 激活函数(优缺点,sigmoid、tanh、relu、gelu)https://zhuanlan.zhihu.com/p/71882757
- sigmoid导数: $y(1-y)$
- tanh 导数: $1-y^2$
- prelu公式: $\max(\alpha x, x)$ 其中$\alpha$ 是可学习的。
- elu公式:$\alpha (exp(x)-1) \text{ where x <= 0}$
- 损失函数(用过哪些损失函数,为啥分类不用MSE): 也就是说,预测错误时,依然没有梯度让网络可以学习。主要原因在于MSE Loss(mean-squared loss)当与Sigmoid或Softmax搭配使用时,loss的偏导数的变化趋势和预测值及真实值之间的差值的变化趋势不一致。也就是说当预测值与真实值的差值变大的时候,其偏导数反而可能变小。 https://zhuanlan.zhihu.com/p/336386852
- 信息论 https://zhuanlan.zhihu.com/p/35379531
- 信息熵:信息量的期望值,同时也可以认为是平均编码长度,将符号转化为log里的-1,就变成了平均编码长度。
- $\mathrm{H}(X)=\mathrm{E}[\mathrm{I}(X)]=\mathrm{E}[-\ln (\mathrm{P}(X))]$ ,
- $\mathrm{H}(X)=\sum_i \mathrm{P}\left(x_i\right) \mathrm{I}\left(x_i\right)=-\sum_i \mathrm{P}\left(x_i\right) \log _b \mathrm{P}\left(x_i\right)$
- https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA)
- 条件熵:
\(\begin{aligned} H(Y \mid X) &=\sum_x p(x) H(Y \mid X=x) \\ &=-\sum_x p(x) \sum_y p(y \mid x) \log p(y \mid x) \\ &=-\sum_x \sum_y p(x, y) \log p(y \mid x) \\ &=-\sum_{x, y} p(x, y) \log p(y \mid x) \end{aligned}\)
- $\mathrm{H}(\mathrm{Y} \mid \mathrm{X})=\mathrm{H}(\mathrm{X}, \mathrm{Y})-\mathrm{H}(\mathrm{X})$
- 联合熵: $H(X, Y)=-\sum_{x, y} p(x, y) \log p(x, y)=-\sum_{i=1}^n \sum_{j=1}^m p\left(x_i, y_i\right) \log p\left(x_i, y_i\right)$
- 相对熵(KL散度):$D_{K L}(p | q)=\sum_x p(x) \log \frac{p(x)}{q(x)}=E_{p(x)} \log \frac{p(x)}{q(x)}$
- 交叉熵: $H(p, q)=\sum_x p(x) \log \frac{1}{q(x)}=-\sum_x p(x) \log q(x)$
- 由此可以看出根据非真实分布 q(x) 得到的平均码长大于根据真实分布 p(x) 得到的平均码长。
- JS散度:kl 散度 p,q 互换相加除以2,解决不对称问题
- https://zhuanlan.zhihu.com/p/240676850
- 信息增益: \(\begin{aligned} g(D, A) &=H(D)-H(D \mid A) \\ &=-\sum P\left(D_i\right) \log P\left(D_i\right)-\sum \frac{\left|D_i\right|}{|D|} H\left(D_i\right) \end{aligned}\)
- 互信息的概念:$I(X ; Y)=H(X)-H(X \mid Y)=H(Y)-H(Y \mid X)=H(X)+H(Y)-H(X, Y) $
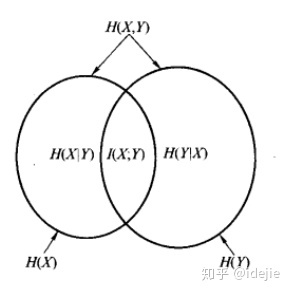
- 说“互信息”的时候,两个随机变量的地位是相同的;说“信息增益”的时候,是把一个变量看成减小另一个变量不确定度的手段。但其实二者的数值是相等的。
-
交叉熵和KL散度区别:DKL(p q)=H(p,q)−H(p)(当用非真实分布 q(x) 得到的平均码长比真实分布 p(x) 得到的平均码长多出的比特数就是相对熵)
- 信息熵:信息量的期望值,同时也可以认为是平均编码长度,将符号转化为log里的-1,就变成了平均编码长度。
- 归一化:
- 为什么要做归一化:https://zhuanlan.zhihu.com/p/265411459
- 加快收敛:特征间的单位(尺度)可能不同, 因尺度差异,其损失函数的等高线图可能是椭圆形,梯度方向垂直于等高线,下降会走zigzag路线,而不是指向local minimum。
- 早期对BN有效性的解释是其有助于缓解神经网络“内部协方差漂移”(Internal Covariance Shift,ICS)问题。即,后面的层的学习是基于前面层的分布来的,只有前面一层的分布是确定的,后面的层才容易学习到有效的模式,然而,由于前面的层的分布会随着batch的变化而有所变动,导致了后面的层看来“前面一直在动,我无法安心学习呀”。
- 什么时候不需要Feature Scaling?:
- 与距离计算无关的概率模型,不需要feature scaling,比如Naive Bayes;
- 与距离计算无关的基于树的模型,不需要feature scaling,比如决策树、随机森林等,树中节点的选择只关注当前特征在哪里切分对分类更好,即只在意特征内部的相对大小,而与特征间的相对大小无关。
- 所以pca,knn,svm等模型必须进行归一化
- 各种归一化的区别和优缺点 https://blog.csdn.net/qq_29367075/article/details/110006934
- Batch Normalization:
- BN的计算就是把每个通道的NHW单独拿出来归一化处理
- 针对每个channel我们都有一组γ,β,所以可学习的参数为2*C
- 当batch size越小,BN的表现效果也越不好,因为计算过程中所得到的均值和方差不能代表全局。
- Layer Normalizaiton:
- LN的计算就是把每个CHW单独拿出来归一化处理,不受batchsize 的影响
- 常用在RNN网络,但如果输入的特征区别很大,那么就不建议使用它做归一化处理
- Instance Normalization
- IN的计算就是把每个HW单独拿出来归一化处理,不受通道和batchsize 的影响
- 常用在风格化迁移,但如果特征图可以用到通道之间的相关性,那么就不建议使用它做归一化处理
- Batch Normalization:
- NLP为啥不用BatchNorm:看了一通还是觉得 科学空间的作者说的有道理,nlp里文本长度有变化其统计量不稳定
- 为什么要做归一化:https://zhuanlan.zhihu.com/p/265411459
- 梯度消失(残差、门控、sigmoid换relu、归一化)
- 梯度爆炸(截断)
- 优化器(原理和演进过程,SGD、AdaGrad、RMSprop、AdaDelta、Adam、
- AdamW: L2 regularization 和 Weight decay不一致
- 显存爆炸(
- 重计算:要保存中间几个检查点的计算数值,所以不用从头开始重新计算,而是只要从检查点开始重新计算就好了欸。真好用
- 梯度累加、混合精度训练、Adam换成SGD、
- 多用inplace:例如relu,直接修改输入值,所以就没有
- 学习率(
- 衰减:
- 指数衰减
- 固定步长衰减
- 余弦退火衰减
- warmup:由于刚开始训练时,模型的权重(weights)是随机初始化的,此时若选择一个较大的学习率,可能带来模型的不稳定(振荡),
- 自适应、
- 平时自己使用的时候对lr有什么调整心得吗)
- 衰减:
- 样本不均衡(降/过采样和带权重的loss)
- 数据预处理(
- 离散特征
- one-hot
- 映射到欧式空间,方便计算距离
- 能够进行归一化
- one-hot
- 连续特征
- 归一化
- 离散化:
- 优点:鲁棒性高;方便增加特征,迭代模型;为逻辑回归模型引入了非线性,提升模型表达能力;便于特征交叉,进一步增加非线性;降低过拟合风险。
- 离散特征
- 评价指标(Acc、Precision、Recall、F1、
- ROC:y:真阳;x:假阳
- AUC:$A U C=\frac{\sum_{i \in \text { posittveClass }} \operatorname{rank}-\frac{M(1+M)}{2}}{M \times N}$
- 代码实现AUC)
- 神经网络(
- 优点
- 缺点:需要数据量大;运算量大;可解释性低;
- 演进和公式推导,lstm、cnn、transformer)
- OOV咋办
- NLP包括两板块,一个是通用的基础(所有面试官都可能问)和你个人研究方向的基础。
NLP
-
个人研究方向基础没啥好说的,比如你做生成,面试官就很可能让你手写beam search;做序列标注的就可能让你推viterbi解码、HMM和CRF区别之类的;做文本匹配可能就问你双塔和concat模型、CLS塌缩和对比学习之类的。这个需要大家根据自身的情况选择性去复习。
- 通用NLP基础我和小伙伴暂时能想起来的主要包括下面这些了。
- 经典模型的原理和手撸代码
- 文本关键词抽取(textrank和tf-idf)
- 词向量模型(NNLM、word2vec和glove)
- 相对于NNLM,word2vec的改进有哪些
- 哈夫曼树的构建方法,在NLP有啥应用
- hierarchical softmax和负采样的原理和复杂度
-
负采样的具体实现方法
-
word2vec和glove的区别
-
怎样评估词向量的质量:https://memo.rstalker.com/others/vector_eval.html
-
选出当前query和100万个key词向量相似度的TopK,复杂度尽可能低(faiss)
-
预训练发展
-
word2vec - glove - ELMo - GPT - BERT - others的演进,每个模型分别解决什么问题
-
Transformer的细节
-
为什么要用多头(多个空间学习多种pattern、降低注意力学习的风险)
-
为什么Q和K的映射矩阵不相同(关系对称、容易得到单位矩阵)
-
为什么注意力权重要除 (防止梯度消失)
-
为什么用乘性注意力不用加性注意力(乘性计算量更小?):https://blog.csdn.net/weixin_37958272/article/details/108396561
-
为什么要有FFN模块(增加模型的非线性能力)
-
Transformer和BERT的位置编码有啥区别(三角函数式和可学习向量)
-
残差结构及意义(防止梯度消失和网络退化)
-
哪个block中更耗时,哪个更占显存(序列短的时候FFN耗时,长的时候MHA耗时;FFN更占显存)
-
transformer的LayerNorm有哪些(post-norm和pre-norm)
-
如何对pad进行mask(将pad的attention_score加上-np.inf,过softmax后会变0)
-
怎样解决曝光偏差(训练时以一定的概率用上一时刻的输出、NAR、占位符生成、基于负梯度构建对抗样本)
-
transformer加速(NAR,知识蒸馏、剪枝、动态退出、稀疏注意力、线性注意力等)
-
attention瓶颈(low rank,talking-head等)
-
BERT的细节
-
BERT怎么做分词(Basic Tokenizer和WordPiece Tokenizer)
-
WordPiece和BPE有啥区别
-
BERT的两个预训练任务分别有啥优缺点,后续有啥改进工作
-
为什么BERT要用自己学习的位置编码(在训练充分的情况下,可学习的比三角函数式的的表示能力要更强)
-
BERT的位置编码有啥缺点,还有哪些位置编码(绝对位置并不能很好的表示距离和方向,后面有相对位置编码、复数位置编码以及加入树形的位置编码等,参考tener,transformer-xl,t5,deberta,tupe和roformer等等)
-
BERT的FFN为啥要用GeLU激活函数(非饱和区大同时非线性也更强?)
- BERT-Related-Works
C++
TODO
- python basics
- c++ interview
- 推荐系统
- 搜索
- NLP
- 机器学习
- hadoop等
- 面经:https://zhuanlan.zhihu.com/p/34953654